사칙 연산 없이 논리 게이트만으로 이진수(비트)의 덧셈을 구현해보겠습니다.
사칙연산 - 덧셈으로부터
컴퓨터의 사칙 연산은 덧셈에서부터 이루어집니다.
우리 컴퓨터가 덧셈은 할 줄 안다고 가정하면,
1. 뺄셈은 보수를 취한 덧셈으로 계산할 수 있습니다.(부호를 나타내는 최상위 비트)
2. 곱셈은 곱하는 수만큼의 덧셈을 반복이며, 이 경우 더한 수를 세주는 계수기(counter)와 가산기가 필요합니다.
3. 나눗셈은 몫이 [1]보다 작아질 때까지 나누어지는 수에서 나누는 수를 계속 빼면서 계수기로 횟수를 세면 됩니다.
그러나 위의 곱셈과 나눗셈은 간단한 수일 경우 문제가 없겠지만 long 단위의 수를 다루게 된다면, 계산 횟수가 기하급수적으로 늘어난다는 문제가 있습니다. 곱셈의 경우, 이진수의 계산이라는 가정하에 매우 간단하게 연산량을 줄일 수 있습니다. 곱셈을 손으로 푸는 과정을 생각해보면, 먼저 한 자리 수와 숫자를 반복해가며 비트 곱하여 아래 그림의 (1)번 행을 계산합니다. 그리고 다음 숫자와 동일하게 곱셈을 반복해서 (2)번 행을 계산하고, 그 결과를 더해서 최종 값을 얻습니다. 이진수의 곱셈은 논리 게이트를 통해서 간단하게 수행할 수 있죠. 즉, AND Gate의 결과와 일치합니다. 그리고 한 줄의 결과를 얻고 다음 자릿수로 바꾸는 행위는 시프터(Shifter)를 통해서 통해서 수행됩니다.

나눗셈도 마찬가지로 이진수인 경우 쉽게 수행할 수 있습니다. 아래 그림처럼, 자릿수를 바꾸는 시프터(Shifter)와 감산기(Subtractor - 결국 가산기를 통해서 구현됨)로 구현할 수 있습니다.

여기까지, 덧셈이 컴퓨터의 사칙연산에 매우 중요한 부분을 차지한다는 사실을 알 수 있었습니다. 그렇다면, 컴퓨터는 덧셈을 어떻게 수행할까요?
가산기란?
가산기의 정의는 아래와 같다.
가산기는 덧셈 연산을 수행하는 논리 회로, 덧셈 연산을 수행하는 논리 회로이며 디지털 회로, 조합 회로의 하나이다. 가산기는 산술 논리 장치뿐만 아니라 주소값, 테이블 색인 등을 더하는 프로세서의 한 부분으로 사용되고 있다. 이진화 십진법, 3 초과 부호와 같은 여러 가지 수학적 연산을 수행하는 가산기를 구성할 수 있지만, 대부분의 가산기는 2진수의 합을 계산한다. 2의 보수나 1의 보수를 이용하여 음수를 표현하는 경우, 가산기를 가감산기로 사용한다. 다른 숫자의 부호 표현의 경우 더 복잡한 가산기를 필요로 한다. [출처 - 위키백과]
초기의 컴퓨터에서는 진공관에 의해 구성되었다고 하며 점차 더 효율적인 집적 회로로 대체되었습니다. 전압의 덧셈을 출력하는 디지털 회로를 가산 회로라고 부릅니다. 컴퓨터는 즉, 0과 1로 이루어진 비트와 가산기를 이용해서 덧셈을 수행합니다.
가산기는 반가산기(Half Adder)와 전가산기(Full Adder)로 나뉩니다.
반가산기(Half Adder)
이진수의 한 자리 수 간의 합을 구하는 논리 회로, 결과 값으로 합(Sum)과 자리올림(Carry)를 산출한다. 입력에 자리올림수가 들어올 수 없으므로 한 자리 수 이진법에만 적용될 수 있습니다.

전가산기(Full Adder)
자리올림 수 C(Carry in), 1비트 이진수 2개, 총 3개의 이진수를 더하여 합과 자리올림수(Carry out)을 구하는 회로로
2개의 반가산기 + 1개의 OR로 구성됩니다. Carry in은 여러 자리 수의 덧셈을 할 때 자릿수가 높아지면 이전 자릿수의 올림 값을 함께 더해주죠? 이전 자리수에서 계산된 올림값(Carry)를 더하는 것을 구현하기 위한 논리 회로입니다. 예로, A = 11, B = 11일때 큰 자릿수의 덧셈에서 올림 값과 큰 자리 수 2개, 총 3개의 수를 더해서 값을 계산하는 것을 생각해보면 이해가 쉽습니다.
세 수를 더해서 Sum과 Carry-out이 1이되는 경우는 어떤게 있을까요? 아래 진리표를 보면, Sum이 1이 되는 경우는 3개의 수 중 홀수 개가 1일 때입니다. Carry-out이 1이 되는 경우는 3개의 수 중 2개 이상이 1일 때입니다. 이를 논리 게이트의 조합으로 나타낸 것이 전가산기입니다.


이러한 전가산기의 조합으로 임의 자리수의 2진수 덧셈을 계산할 수 있습니다.
리플 자리 올림수 가산기
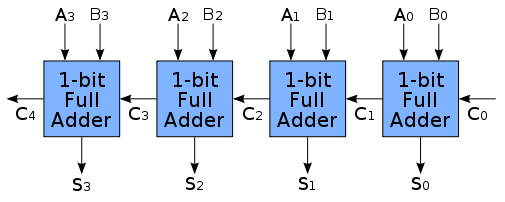
각각의 전가산기가 자리올림수 입력 Cin으로 직전의 자리올림수 출력 Cout을 받는 형식으로, 자리올림수가 물결(ripple)치듯 다음 가산기로 옮겨 간다고 하여 리플 캐리 가산기라 합니다. 아래 그림은 4비트 가산기의 회로도입니다. 이해를 돕기위해 (1111 + 1111)을 계산한다고 해봅시다. 아래 그림에서 C0, C1, C2, C3, C4는 각각 (0,1,1,1,1)에 해당 될 것입니다. 그리고 합에 해당하는 S0, S1, S2, S3는 각각 (0, 1, 1, 1)이므로 C4S3S2S1S0를 순서대로 읽으면 11110(2)가 되며 이는 실제로 1111+1111을 이진 덧셈한 결과 값과 같습니다. 즉 논리 게이트만으로 이진법의 덧셈 구현이 가능한 것입니다.

이진수의 덧셈 구현(Java)
public boolean[] sumBinary(boolean[] a, boolean[] b) {
boolean[] result = new boolean[MAX_ARRAY_SIZE];
a = init(a);
b = init(b);
List<Boolean> output = halfAdder(a[0], b[0]);
boolean carryIn = output.get(CARRY);
result[0] = output.get(SUM);
for (int index = 1; index < MAX_NUMBER_SIZE; index++) {
output = fullAdder(a[index], b[index], carryIn);
result[index] = output.get(SUM);
carryIn = output.get(CARRY);
result[index + 1] = carryIn;
}
return result;
}
다음으로 반가산기 메소드를 상세 구현해보겠습니다. XOR와 AND 비트 연산자를 사용해주고 결과 값인 Sum과 Carry를 링크드리스트에 저장해서 반환해줍니다.
private List<Boolean> halfAdder(boolean a, boolean b) {
final boolean sum = a ^ b; //SUM은 XOR
final boolean carry = a & b; //CARRY는 AND
List<Boolean> output = new LinkedList<>();
output.add(sum);
output.add(carry);
return output;
}
비슷하게 전가산기 메소드 구현입니다. XOR와 AND, OR연산자의 결합으로 결과 값인 Sum과 Carry를 링크드리스트에 저장해서 반환해줍니다.
private List<Boolean> fullAdder(boolean a, boolean b, boolean cin) {
final boolean sum = a ^ b ^ cin; //SUM은 XOR
final boolean carry = (a & b) | (b & cin) | (cin & a); //CARRY는 (A&B) OR (B&C) OR (C&A)
List<Boolean> output = new LinkedList<>();
output.add(sum);
output.add(carry);
return output;
}
이상으로 컴퓨터의 덧셈 로직을 알아보았고 덧셈에 필요한 장치인 전가산기, 반가산기의 작동 로직을 살펴보았습니다. 최종적으로 이를 그대로 논리 연산자를 활용해서 자바로 구현까지 해보았습니다.
'Computer Science > 기타' 카테고리의 다른 글
| 오토마타 이론과 Parser의 원리 - HTML Parser 만들기 (Java) (0) | 2023.02.01 |
|---|---|
| 함수형 프로그래밍 입문 with 람다 대수, 함수형 인터페이스 (Java) (1) | 2023.02.01 |
| 객체지향 설계 연습(SOLID, GRASP) - 좌표평면 도형 그리기 (Java) (2) | 2023.01.28 |
| 프로세스의 메모리 영역 (Heap, Stack) 구현하기 (Java) (0) | 2023.01.15 |
| 미니 16비트 CPU + 메모리 구현해보기 (Java) (0) | 2023.01.14 |


